The Two Crystal Balls Problem: Why Sometimes Being Smart Means Taking Baby Steps 🔮✨

What if I told you that the secret to solving one of computer science’s trickiest puzzles was discovered by… being more careful with your resources? 🤯

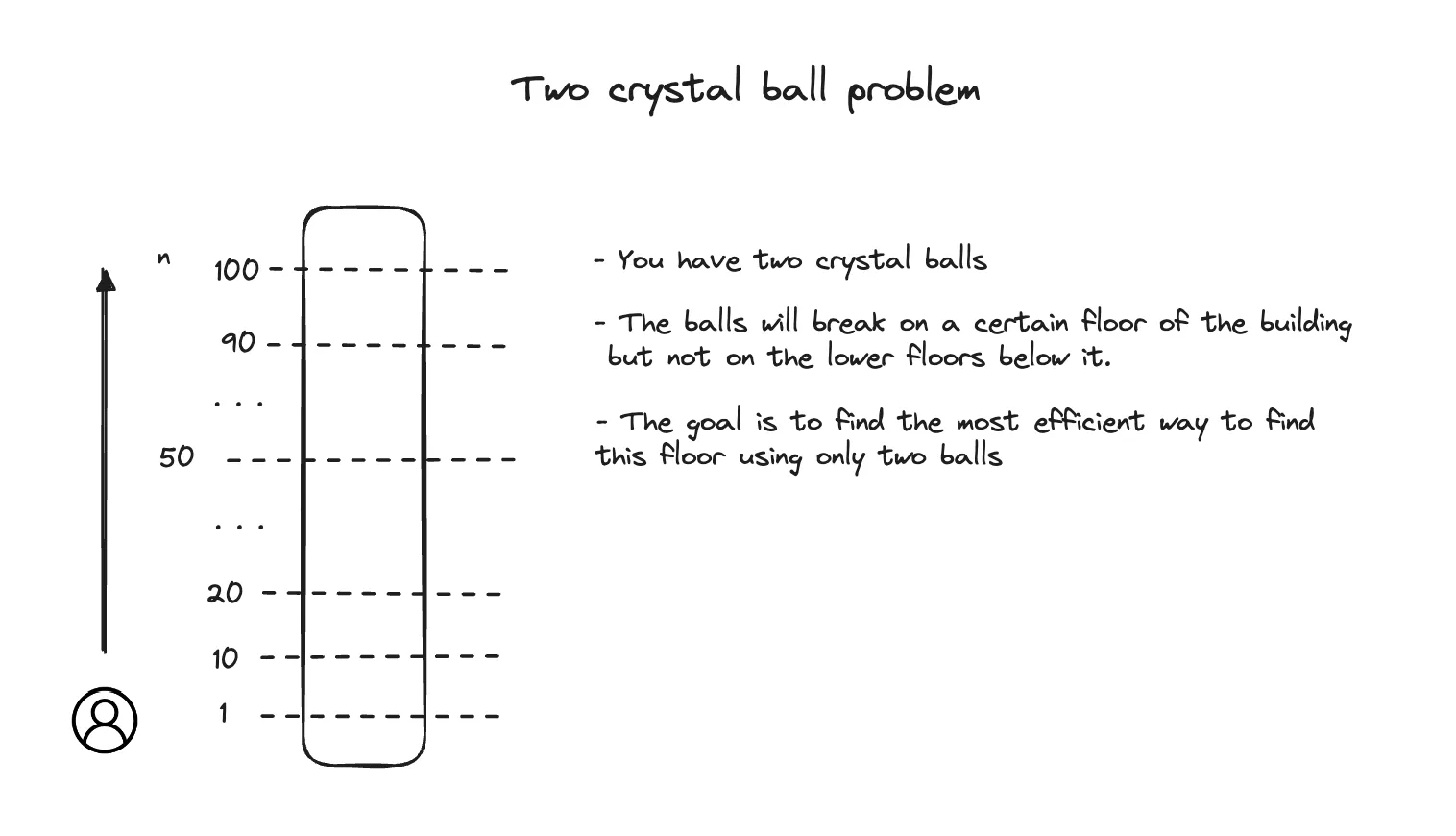
Imagine you’re standing on top of a skyscraper with two priceless crystal balls, and one wrong move could cost you everything. This isn’t just a thought experiment – it’s a problem that teaches us something profound about decision-making under pressure, and the solution will change how you approach challenges in your everyday life 💡.

Have you ever been in a situation where you had to be really, really careful because you only got one shot at getting it right? Maybe you were hanging a heavy picture and only had one good nail 🖼️, or trying to parallel park in the only available spot on a busy street 🚗. Well, computer scientists have a puzzle just like this, and it’s way more interesting (and useful) than you might think! 🤓

The Setup: A Tale of Two Very Expensive Crystal Balls 💎

Picture this: You’re standing in a 100-story skyscraper with two beautiful, incredibly expensive crystal balls 🏗️🔮🔮. These aren’t your average crystal balls – they’re special. They have a magical property: they’ll break if you drop them from a certain floor or higher, but they’ll survive perfectly if dropped from any floor below that mystery breaking point ✨.

Your job? Figure out exactly which floor is the “breaking floor” – but here’s the kicker: you only have those two crystal balls 😰. Once they’re both broken, game over 💥. You can’t just go buy more at the crystal ball store (if only it were that easy! 😅).

Think of it like this: imagine you’re trying to figure out how much weight your old wooden shelf can hold before it breaks, but you only have two identical heavy books to test with 📚📚. You want to find the exact breaking point, but you can’t afford to waste your test materials 🤷‍♀️.

The Obvious (But Wrong) Approach 🚫

Your first thought might be: “Easy! I’ll just start in the middle – floor 50 🎯. If it breaks, I know the answer is somewhere between floors 1-50. If it doesn’t break, it’s between floors 51-100.”

This is actually brilliant thinking – it’s called binary search, and it’s one of the most elegant problem-solving strategies in all of computer science 🧠✨. It’s like that game where someone thinks of a number between 1 and 100, and you try to guess it 🎲. You’d start with 50, right?

But here’s where our crystal ball problem gets tricky 😬. Let’s say you drop your first ball from floor 50 and… CRASH! 💥 It shatters into a million pieces. Now you know the breaking floor is somewhere between 1 and 49, but you only have one ball left 😱.

What do you do now? You’re forced to test every single floor starting from floor 1: drop from floor 1 (safe ✅), floor 2 (safe ✅), floor 3 (safe ✅)… and so on until CRASH! 💥 goes your second ball. In the worst-case scenario, you might end up testing 49 floors just to find your answer. That’s a lot of drops for someone who started with only two crystal balls! 😵‍💫

The “Aha!” Moment: Think in Chunks, Not Halves 💡

Here’s where the magic happens ✨. Instead of cutting the problem in half, what if we thought about it in chunks? 🧩

The brilliant insight is this: use $\sqrt{n}$ as your chunk size. For a 100-story building, $\sqrt{100} = 10$. So instead of starting at floor 50, we start at floor 10 🎯.

Here’s how it works:

• Drop your first ball from floor 10. Safe? Great! ✅
• Try floor 20. Still safe? Awesome! ✅
• Keep going: 30, 40, 50, 60… 🚀
• Let’s say it breaks at floor 60 💥. Now you know the breaking floor is somewhere between floors 51 and 60.

Now comes the second phase: take your remaining ball and test floors 51, 52, 53… until it breaks 🔍. In the worst case, you’ll test 10 floors in the second phase.

Total drops in the worst case: 10 (first phase) + 10 (second phase) = 20 drops 🎉. Compare that to the potentially 50 drops from the binary search approach! 📊

Why This Works: The Math Made Simple 🔢

Don’t worry – no complex equations here 😌. The math is actually pretty intuitive.

Think of it like organizing a library 📚. If you have 100 books and want to find a specific one, you could:

1. Check every book one by one (up to 100 checks) 😴
2. Split the pile in half repeatedly (but risky if you can only handle books a few times) 😰
3. Divide into 10 piles of 10 books each, find the right pile, then search within that pile (at most 20 checks) 🎯

The square root approach gives us the best balance between the number of “big jumps” we take and the number of “small steps” we might need afterward ⚖️. Mathematically, it minimizes our maximum possible drops to $2\sqrt{n}$ 📈.

Let’s Walk Through the Code (Don’t Panic!) 🤖

Here’s the javascript that solves this problem:

export default function two_crystal_balls(breaks: boolean[]): number {
  const breakAmount = Math.floor(Math.sqrt(breaks.length));
  
  let i = breakAmount;
  for (; i <= breaks.length; i += breakAmount) {
    if (breaks[i]) {
      break;
    }
  }
  i -= breakAmount;
  for (let j = 1; j <= breakAmount; j++, i++) {
    if (breaks[i]) {
      return i;
    }
  }
  return -1;
}

Let me translate this into human speak 🗣️:

1. Line 2: “Figure out how big our jumps should be” 📏 – that’s our $\sqrt{n}$ calculation
2. Lines 4-8: “Take big jumps until something breaks” 🦘 – this is like testing floors 10, 20, 30, etc.
3. Line 9: “Oops, go back to the last safe spot” ⬅️ – step back to the previous interval
4. Lines 10-14: “Now take small steps until we find the exact breaking point” 👣
5. Line 15: “If nothing ever breaks, return -1” 🤷‍♂️ – our crystal balls are apparently indestructible!

This Isn’t Just About Crystal Balls 🌍

You might be thinking, “This is cool and all, but when am I ever going to need to drop crystal balls from buildings?” 🤔 Fair question! But this problem pattern shows up everywhere in real life:

Software Testing 💻: Imagine you’re launching a new app and want to know how many users it can handle before it crashes. You can’t just throw millions of users at it right away (that would be expensive and embarrassing 😬). Instead, you might test with 1,000 users, then 10,000, then 100,000, using a similar stepping strategy.

Medical Research 💊: When testing a new medication, researchers need to find the optimal dose. Too little won’t work, too much could be dangerous ⚠️. They use careful stepping strategies similar to our crystal ball approach.

Online Shopping 🛒: Ever notice how some websites test different versions of their pages to see which one sells more? They use smart strategies to find the best design without wasting too much time or money on bad versions.

Even Dating Apps 💕: Some apps test different matching algorithms by gradually rolling them out, using principles similar to our crystal ball problem to find what works best.

The Bigger Picture: When Less Really Is More 🎯

The beautiful thing about the two crystal balls problem is that it teaches us something profound about problem-solving: sometimes having fewer resources forces us to be more creative and actually leads to better solutions 🚀.

If we had unlimited crystal balls, we’d probably just use that binary search approach without thinking much about it 🤷‍♀️. But because we’re constrained to just two balls, we discovered a strategy that’s not only more reliable but also teaches us to think about problems in a completely different way 🧠.

It’s like the old saying: “Necessity is the mother of invention” 💡. Our crystal ball constraint didn’t make the problem harder – it made the solution more elegant ✨.

Try It Yourself! 🎮

Next time you’re faced with a problem where you have limited resources or chances to get something right, remember the crystal balls 🔮. Ask yourself:

• Can I break this into smart chunks instead of just diving in? 🧩
• What’s my “worst-case scenario” and how can I minimize it? 🛡️
• Is there a way to gather information in stages rather than betting everything on one approach? 📊

Whether you’re planning a budget 💰, learning a new skill 📖, or even just trying to find the perfect restaurant in a new city 🍽️, the crystal ball strategy of “strategic steps” often beats the “go big or go home” approach.

The Bottom Line 📝

The two crystal balls problem isn’t really about crystal balls at all – it’s about smart resource management 📈, strategic thinking 🧠, and finding elegant solutions under pressure 💎. It reminds us that sometimes the most sophisticated approach isn’t the most complex one, but the one that carefully balances risk and reward ⚖️.

Plus, now you have a great conversation starter for your next dinner party 🍽️: “Hey, want to hear about this fascinating crystal ball problem?” Trust me, people will be more interested than you think! 😉✨